Definición 1.1 (Transformada integral) La transformada integral 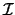 respecto el núcleo
respecto el núcleo 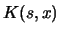 en el intervalo
en el intervalo 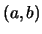 de la función
de la función 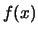 se define de la forma
se define de la forma
![$\displaystyle \bar{F}(s) = \mathcal{I} \big[ f(x) \big] = \int_a^b\!\!f(x) K(s, x) \ensuremath{\mathrm{d}x} . $](http://www.lawebdefisica.com/apuntsmat/trans/img5.png)
Donde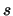 es la variable transformada.
es la variable transformada.
![$\displaystyle \bar{F}(s) = \mathcal{I} \big[ f(x) \big] = \int_a^b\!\!f(x) K(s, x) \ensuremath{\mathrm{d}x} . $](http://www.lawebdefisica.com/apuntsmat/trans/img5.png)
Donde
El operador de transformación 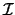 es lineal, así como el operación de transformación inversa
es lineal, así como el operación de transformación inversa 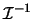 .
.
No hay comentarios:
Publicar un comentario