3.15 ALGUNAS TRANSFORMADAS INVERSAS

Transformada inversa

Se dice que f(t) es la transformada inversa de Laplace de F(s) y se expresa:

Algunas transformadas inversas

3.10 TEOREMA DE LA CONVOLUCION

3.9 TRANSFORMADA DE INTEGRALES (TEOREMA)

Definición 1.1 (Transformada integral)   La transformada integral  respecto el núcleo  en el intervalo  de la función se define de la forma

Donde  es la variable transformada.

El operador de transformación  es lineal, así como el operación de transformación inversa  .

3.8 TRANSFORMADA DE DERIVACIONES (TEOREMA)

TEOREMA 2: Transformada de una derivada

Si , ',….,(n-1) son continuas en [0,"), son de orden exponencial y si (n) (t) es continua por tramos en [0, "), entonces L { (n) (t) }= sn F(s) - s(n-1) (0) - s(n-2) '(0)-…- (n-1)(0). Donde F(s) = L { (t) }.

3.7 TRANSFORMADA DE FUNCIONES MULTIPLICADAS POR TN, Y DIVIDIDAS ENTRE T.

3.10 Teorema de la convoluciòn

En matemática, el teorema de convolución establece que bajo determinadas circunstancias, la Transformada de Fourier de una convolución es el producto punto a punto de las transformadas. En otras palabras, la convolución en un dominio (por ejemplo el dominio temporal) es equivalente al producto punto a punto en el otro dominio (es decir dominio espectral).

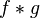Sean f y g dos funciones cuya convolución se expresa con . (notar que el asterisco denota convolución en este contexto, y no multiplicación; a veces es utilizado también el símbolo ). Sea el operador de la transformada de Fourier, con lo que y son las transformadas de Fourier de f y g, respectivamente.

Entonces

donde · indica producto punto. También puede afirmarse que:

Aplicando la transformada inversa de Fourier , podemos escribir:

3.9 Transformada de int5egrales (teorema)

La teoría de las transformadas integrales, en especial, de la transformada de Laplace y la de Fourier. La transformación de Laplace es de amplia aplicación en el campo de la electrónica y l teoría de circuitos. Por otra parte, la transformada de Fourier, es de amplia aplicación en el análisis de señales, así como en diferentes campos de la física (teoría de la difracción, mecánica cuántica, etc.). Las transformadas integrales se presentan en forma de apuntes esquemáticos y sin demostraciones.

Definición 1 (Transformada integral)   .1La transformada integral respecto el núcleo en el intervalo de la función se define de la forma

 

Donde es la variable transformada.
El operador de transformación es lineal, así como el operación de transformación inversa .